 Analogy
Analogy In order to explain our table of knots, we have to describe the notion of prime knot. This is done by
explaining a basic way of combining knots.
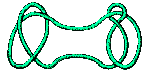
Trefoil + Figure Eight
Given any knots K and L we call this process of combination addition of the two knots and write it as K + L .
There was a decision to be made here: whether to call the combination of knots 'addition' or 'multiplication'. The literature uses both terms.
We chose the term addition for two reasons. One was that the notation
0 for the unknot is more descriptive than the notation 1.
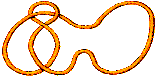
K + 0 = K
The more important reason was to emphasise that the analogy is not between things but between the way things behave, between their relationships. So when we make an analogy between Trefoil + Figure Eight and 2 x 3 we are not saying that the number 2 is analogous to the Trefoil, but that the combination +of knots has properties analogous to those of the product x of numbers.
To make this point, it is helpful to have a different notation for the two operations which are being taken as analogous. Using the term addition of knots, we make an analogy between an addition and a multiplication. This, we hope, is more striking and also illustrates a general point, that such analogies may be available in other situations.
Although we use the term "The arithmetic of knots", we also use algebraic notation and emphasise laws.
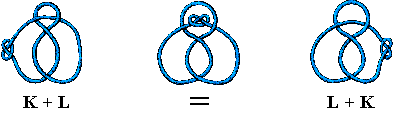
Note here that we are using a particular example to illustrate a general law, the commutative law for addition of knots. This makes the point that it is as the study of analogies that algebra obtains its generality and power. When we say that for numbers m, n we have
m + n = n + m, m x n = n x m
we are making an analogy between the properties of addition and of multiplication. Note also that we make a leap from instances of these laws such as
2 + 19 = 19 + 2, 27 x 51 = 51 x 27
to the general statements, about all numbers.
By using the commonplace word "analogy", we aim to demystify, and to show that one aspect of the method of algebra is as a standard process by which we understand and try to make order of the world. The other point to be made is of course the excitement of an unexpected analogy, of "That reminds me of ...!".
We are also able to illustrate the deep fact that knots have a decomposition into a sum of prime knots, and this decomposition is 'unique up to order'. Note that these words 'up to order' have a familiar meaning to a mathematician, but will be unfamiliar in this sense to the general public. This is why we give illustrations of the fact rather than its general statement.
The appreciation of this decomposition led one small boy after a Mermaid Molecule Discussion by R.B. in 1985 to ask: "Are there infinitely many prime knots?". It so happened that the lecturer had not previously formalised the question for himself, so had really to think in order to be clear that all torus knots are prime, and that there are an infinite number of them. However the proof that torus knots are prime is not so easy. It is good to have something to state which is comprehensible and believable, but which it is not at all clear how it might be proved. This is one of the great advantages of knot theory for expositions at this level.
| Arithmetic of Knots | Knots and Numbers |
© Mathematics and Knots, U.C.N.W.,Bangor, 1996 - 2002
This material may be used freely for educational, artistic and
scientific purposes, but may not be used for commercial purposes,
for profit or in texts without the permission of the publishers.