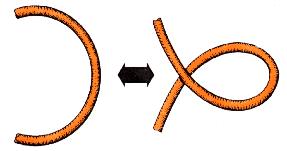
In this case we stay with one colour
on both sides
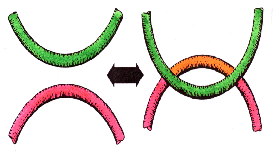
On the right we have three colours,
and on the left no crossing
It does not matter which picture of a knot we try to colour. Either all pictures of the same knot can be 3-coloured, or none of the pictures can be 3-coloured. To find out why this is so, let us see what happens when we change a diagram of a knot by our simple moves.
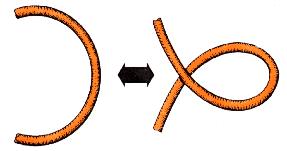
In this case we stay with one colour
on both sides

On the right we have three colours,
and on the left no crossing
We show below two of the many different cases involving the third sort of move. Note that you are always allowed to change some colours at a move, but you still have to keep to the basic rule: at each crossing, there must be either one colour or three colours. This can be done for each move. So we see that a picture that is not 3-colourable cannot be a disguised trefoil.


What about other types of colouring? It is interesting to experiment with more than 3 colours, in the same way, but it has been found that this does not directly give a knot invariant. Instead one has to use a more subtle kind of labelling, which does give new invariants. Try experimenting with different colourings of the following knots, and other diagrams of them.
© Mathematics and Knots, U.C.N.W.,Bangor, 1996 - 2002
This material may be used freely for educational, artistic and
scientific purposes, but may not be used for commercial purposes,
for profit or in texts without the permission of the publishers.