Mirror Images

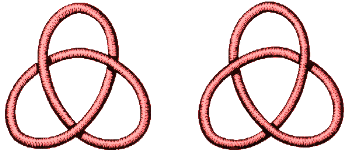
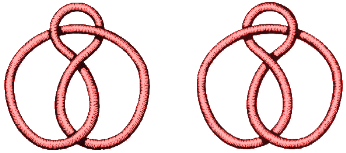
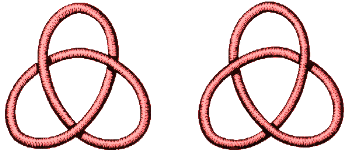
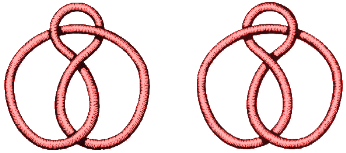
Here are diagrams of trefoils and figure eights. In each case we show a knot and its mirror image. The two trefoils are distinct: however much you twist and pull a trefoil, it will never become its mirror image. However the two figure eights are the same as we can show by the following moves:

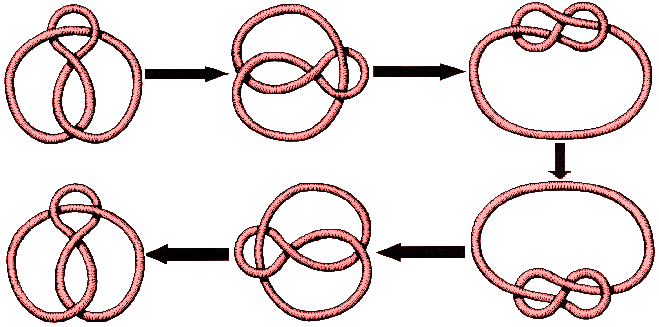
This illustrates a major point. To show that two diagrams represent the same knot, you just have to move one around until you have managed to form the other. If (after a while) you have not succeeded, you may not have been clever enough, or the knots may really be different. The hard thing is to show that two knots are different. For this you need the notion of an invariant, sometimes which will distinguish one knot from the other, whatever the particular form you are given. In 1984 a whole new range of invariants were discovered. For the trefoil and its mirror image the invariants are

This is one way of knowing that no method of twisting and pulling will ever turn a trefoil into its mirror image. l ²m ²- 2 l ²- l ⁴
l ^-2m ² - 2 l ^-2- l^{- 4}

This is one way of knowing that no method of twisting and pulling will ever turn a trefoil into its mirror image.	l ²m ²- 2 l ²- l ⁴	l ^-2m ² - 2 l ^-2- l^{- 4}

It will be difficult for a non mathematician to understand what these strange polynomials

l ²m ²- 2 l ²- l ⁴

l ^-2m ² - 2 l ^-2- l^{- 4}

mean, or how you could calculate them. But you can see that in the first we have l ² and in the second l ^-2. That is, from the first formula to the second the change is exactly that all the powers of l have changed sign. This corresponds to the fact that one knot is the mirror image of the other.

Classification

| Previous | Next |

© Mathematics and Knots, U.C.N.W.,Bangor, 1996 - 2002
This material may be used freely for educational, artistic and scientific purposes, but may not be used for commercial purposes, for profit or in texts without the permission of the publishers.