
|
|
|
| The Golden Mean has value: | 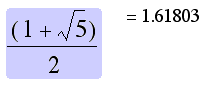 |
|
The golden mean possesses the following unique and exceptional property. If one constructs what is called a golden rectangle, that is to say, a rectangle for which the ratio of the sides a/b is equal to the golden mean (fig1) and if a square is removed from it, one obtains again a golden rectangle (the ratio c/d is still equal to the golden mean), as in fig 2. In other words, this new rectangle has the same proportions as the initial rectangle. It is important to note that this characteristic is only true for the golden rectangle. For example, if a square is removed from the arbitrary rectangle of fig 3, one does not at all obtain a new rectangle having the same proportions as the initial one. Let's return to the golden rectangle and to the passage from fig 1 to fig 2. Since the process is true for all golden rectangles, then one can repeat it and remove a new square from rectangle "cd": one obtains once more a smaller golden rectangle (fig 4). |
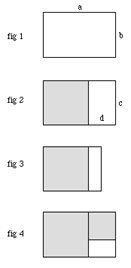 |
| This process can be repeated to infinity to obtain in this way a series of nested rectangles, one inside the other in the form of a spiral (fig 5). | 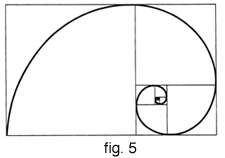 |
This very special spiral (called the logarithmic spiral) is exactly that of the nautilus shell and of certain snails (the planorbe or flat snail). One finds it also in the horns of certain goats (markhor, girgentana), in the shape of certain spider's webs, as well as the takeoff line of certain colonies of bat.
Notice that this spiral (as well as the infinite series of nested rectangles) is an example of a self-similar object, that is, of a structure which is repeated in the same way, but smaller and smaller, at all scales (like the fern represented on another of the posters). In fact, this auto-repetition of the same pattern is actually reflected in the mathematical structure of the golden mean (see below).
Apparently, Stradivarius would have used the golden mean in the construction of his violins. The position of the two holes in the form of an " f " on the top of the violin is of prime importance for the beauty of the sound, and Stradivarius would have used the golden mean in order to calculate their positioning (The New Oxford Companion to Music, vol 2, p. 1927). Let's mention nevertheless that there is no mathematical foundation for this use of the golden mean : although the position of the f-holes is of great importance, it is not clear that this importance is really connected to the golden number. Moreover, the majority of violins today do not make use of this number. But it is true that according to the experts, their sound is not as beautiful as that of a Stradivarius...
THE GOLDEN MEAN AND THE FIBONACCI NUMBERS
One can see the "fractal" structure of the golden mean by writing it in the form of a continued fraction:
In addition, when one takes successive approximations of this series, one recovers the Fibonacci numbers (or more precisely, the ratios of these numbers):
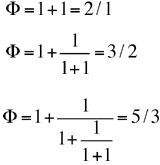
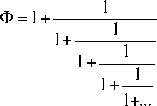
etc.
© Mathematics and Knots, U.C.N.W.,Bangor, 1996 - 2002
This material may be used freely for educational, artistic and
scientific purposes, but may not be used for commercial purposes,
for profit or in texts without the permission of the publishers.