The MÖBIUS Band

Here is how to make a Möbius Band.

Take a long strip of paper,and glue the ends together, but with a twist through 180 degrees.The result might be something like this.

---

Möbius Bands also had an important industrial use when heavy machinery was driven by drive belts from a central power source. These belts could be made to last longer by making them in the form of a Möbius Band. Can you explain why?

---

• Cut your Möbius Band down the middle. What results?
• Next cut your new strip down the middle again. What results?

• Make another Möbius Band. Cut it not down the middle but one third from the edge. What results?

• Form another strip of paper, and this time glue the ends together with a twist of 540 degrees. Again we have a surface with one edge and one side.
  It also is a Möbius Band, but the way it is put into our three dimensional space is different from the previous one.
  This makes an important distinction: between the object itself, and the way it is a part of a space.

• Cut this new object down the middle. What results?

There is another way of thinking of the structure of the Möbius Band, which corresponds to the way we made it from a strip. The Band has a middle circle, which goes round the Band only once. Notice that there are other circles, seemingly parallel to the middle one, but which go round the Band twice. Now draw lines on the Band at right angles to the middle circle. For each point of the middle circle we have a line, and as this line moves around the middle circle, it twists. This gives a mathematical model of the Möbius Band which we can realise in a picture. Here are four views of the Möbius Band.

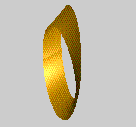
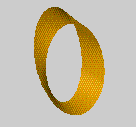
and a 3D rotating picture (90Kb) :

There is information explaining how we made the pictures,notes for doing the same with some of John Robinson's sculptures, and examples, such as a 3D rotating DEPENDENT BEINGS

We have also found another interesting picture of the Möbius Band, and it is in the Geometry Center Graphics Archive (outside link).

Here is another experiment, either in practice or a thought experiment. Make a  Möbius Band out of cloth, and make a disc of cloth whose edge is the same length as the edge of your Möbius Band. Now try and sew the two together along their edges. What happens?

What you are trying to make is called a Projective Plane