JOURNEY and the BREHM model
of the MÖBIUS band

In 1990 Ronnie Brown visited John Robinson with the French geometer Bernard Morin who has been blind since the age of 5. John laid out a range of maquettes for Bernard to see with his hands.

One of the perceptive comments Bernard made was that John was a modest person, as shown by the way he can obtain an effect without dazzling technical means. An example is Eclipse (not shown here) which is made from two offset hemispheres of bronze, with differing surfaces.

Bernard Morin showed us the Brehm model of the Möbius Band, and JOURNEY is John Robinson's version of this.


BUT WHAT IS THE BREHM MODEL ?

There is a space known to Mathematicians as the " Projective Plane". It has relations to the notion, used in technical drawing of projection, which concerns looking at a model or object from different viewpoints.

However there is no way of building this projective plane in our 3-dimensional space. This is a mathematical fact, a theorem, but a little experiment will convince you that a disc of cloth cannot be sewn onto the edge of a möbius band. The way in which an attempt at this process gets tangled up shows that there might be a model which crosses itself.

The first of these models was produced by Boy, a student of Hilbert, at the end of the last century. A remarkable model with flat faces has recently been discovered by U Brehm. First one makes three "horses heads".

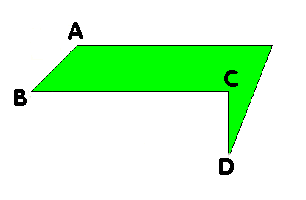
The crucial feature of these is that the lengths of the parts AB and CD are to be the same. Also there is a right angle at BCD. These three horses heads are glued together so that the part AB of one is attached to CD of another.The result is a Möbius Band. You can make this model for your self

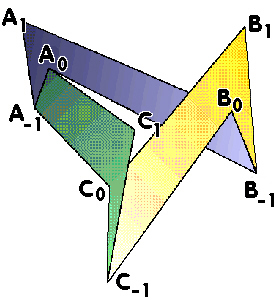
Now to form the projective plane, seven more triangles have to be added.

Four of them,
A-1 B-1 C-1
and
A1 A-1 C-1,
B1 B-1 A-1,
C1 C-1 B-1
are added on the outside and cause no problems, but it is a good idea to cut a hole in the middle of the first triangle so that you can see inside.

The three interior triangles
A1B0 C-1,
B1C0 A-1,
C1A0 B-1,
intersect each other and the three horses, so to make the model you have to cut holes in the triangles. Detailed instructions for making this model are in Brehm's article.

With respect to edges, this means: we add to the three horses heads the following edges:

On the one hand, the boundary of the first triangle mentioned above, namely
A-1 B-1,   B-1 C-1,    C-1A-1
as well as
A1C-1,   B1A-1 ,   C1B-1.

Reference: Brehm, Ulrich: How to Build Minimal Polyhedral Models of the Boy Surface, The Mathematical Intelligencer Vol. 12, 51-55 (1990)

© Mathematics and Knots/Edition Limitee 1996 - 2002
This material may be used freely for educational, artistic and scientific purposes, but may not be used for commercial purposes, for profit or in texts without the permission of the publishers.