How we made the Pictures

The more elaborate animations by Nick Mee were made using POVRAY. However we can give more detail of the methodology of the other animations.

Some of John's sculptures have a precise mathematical description: this is so for example for ETERNITY, GORDIAN KNOT, DEPENDENT BEINGS, MUSIC OF THE SPHERES, RHYTHM OF LIFE (see below for links). All of these may be described as `fibre bundles', with base a circle, and a 2-dimensional shape, called the fibre, which is slotted onto the circle and twists as it moves around. The fibre bundle needs for its description the base, fibre, and the amount of twist. Amazingly, this mathematical description corresponds precisely to how the first four of these were made! The interesting point is that so many beautiful objects which stir the imagination are described by simple exact formulae.

The original animations for this web site were constructed in 1996 using the drawing facilities of a symbolic computation package called AXIOM, with its supplied facilities for making tubular surfaces, and extra code by Larry Lambe for exporting to GEOMVIEW, which gives a lot of control over various aspects of the figure.

For us, the advantages of AXIOM as a symbolic computation package were: (i) all mathematical and datatype code is open, and so can be modified and adapted for new purposes, (ii) the strongly typed language, with parametric datatypes, inheritance, and coercion, makes it appropriate for dealing with mathematical structures, i.e. for dealing with mathematics, (iii) it was available, due to an EPSRC grant to R. Brown and T. Porter for work in `Non abelian homological algebra', (iv) the already written code in ntube.inputs and in the export to GEOMVIEW files of Larry Lambe were exactly suitable for the purpose in hand. Unfortunately, AXIOM is no longer commercially available. However we give some description of the methodology to illustrate the mathematical principles.

ntube.inputs

This file allows the specification of a base 3-dimensional curve, called here the space curve; in all the five examples here, the space curve is a circle, given by the formula [4*cos(t),4*sin(t),0], for a range of values of t. Next one specifies a 2-dimensional curve, giving the shape of the `fibre'. There are several ways of specifying this for the given results, for example by specifying the fibre as a square, triangle, and so on. We are able to specify a twisting function, which rotates the plane curve by some function depending on t as the plane curve moves along the space curve. Because of this twisting, it was possible to specify the plane curve in a simpler fashion, as only a part of the fibre, but allowing a multiple traverse of the space curve.

A final point of information is the number of steps for each of the u and t variables. The payoff here is that a small number of steps leads to a quickly executing program, but the result can be jagged. The effect is often interesting, but not what was intended as a model of the sculpture. A small amount of jaggedness will be smoothed satisfactorily in the GEOMVIEW program.

The details are as follows:

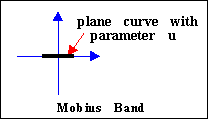
Möbius Band

The space curve is a circle, radius 4, traversed for t from 0 to 2p. The plane curve is the line segment on the x-axis from -1 to 1. The twisting is by t/2. (That page contains an animation.)

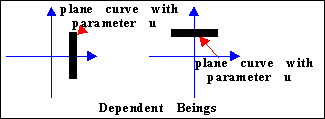
Dependent Beings

This is made of two Möbius bands put together, rather than a twisting square, since this is simpler to code and also allows the two bands to be of different colour, as in the sculpture.(We made an animation of this, and also there is Nick Mee's animation.)

Eternity

The plane curve is given in complex number notation by (1-u) +uw, where 0 £ u £ 1, and w is the complex cube root of 1. (Here £  means `less than or equal to'.) The range of t is from 0 to 6p, and the twist is by t/3. See Nick Mee's animation.

Music of the Spheres

The base circle is of radius 4, traversed 3 times. The plane curve is given by [1+ cosu, sinu] if 0 £ u £ 2p/3, and by [cos(-u +p/3), sin(-u+p/3) +…[ 3] ] for 2p/3 £ u £ 4p/3. The twisting is by t/3. See Nick Mee's animation.

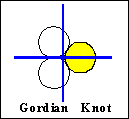
Gordian Knot

The base circle is of radius 5, traversed 3 times. The plane curve is the circle [cosu + 2/…3 , sinu] centre ((2/…3), 0) and radius 1, and the twist is by 8t/3. (See also Nick Mee's animation.)

Rhythm of Life

The base circle is of radius 2, traversed 4 times. The plane curve is a rectangle centre (1,0) and of sides 0.4 and 0.1. The twisting is by 15t. See Nick Mee's animation.

Bonds of Friendship

This is obtained by creating two toruses in 3-space, using the draw function, with a tube around the curve. The radius of each tube is 0.5, and one of them is given by the curve (sin(t),cos(t),0) and the other by the curve (0,1+sin(t), cos(t)). See Nick Mee's animation

Immortality

Here it was necessary to take the space curve to be a trefoil knot, and the plane curve to be a rectangle. We found it difficult to model the sculpture exactly, since the trefoil curve as used by John was not described by the simple mathematical formulae we tried. Also, the twisting of the curve was unduly reflected in the twisting of the rectangle, and so again the formulae we used does not give an exact model. To do so, a lot more experimentation would be needed. So the animations here are by Nick Mee. See Nick Mee's animation