Torus Knots
(Page 1 of 2)
Torus is the mathematical name for an inner tube or doughnut.


Torus is the mathematical name for an inner tube or doughnut.


It is obtained by rotating a circle a fixed distance from the origin (see Fibre Bundles ). John Robinson's BONDS OF FRIENDSHIP consists of two linked toruses.
John describes how he made RHYTHM OF LIFE by wrapping ribbon around an inner tube and was totally surprised when it met up with itself.- see the animation too. Here is a picture of what he did using a tube rather than a ribbon. We show it with and without the torus and in different positions. It is called a (15,4) torus knot, because it is wrapped 15 times one way and 4 times the other. Check how these numbers arise in the picture.
Without Torus


With Torus


Here is what a (4,15) torus knot looks like !


You can make a torus knot T(p,q) with any numbers p, q provided they are coprime, i.e. have no common divisor - so (2,6) will not do. The pair (15,4) is interesting because it uses the three prime numbers 2, 3, 5.
Here is an animation (120k) and some pictures of an (8,3) torus knot.
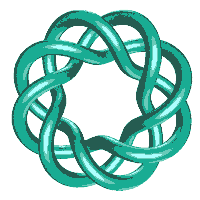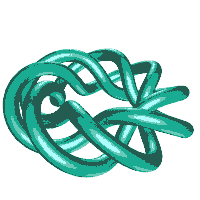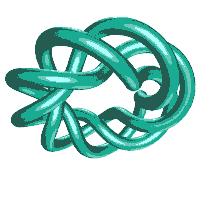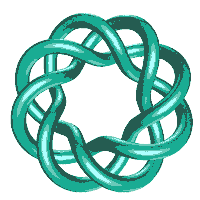
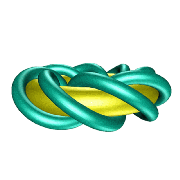


The GORDIAN KNOT is also an (8,3) torus knot, but with a thick tube, and an invisible inner torus! (There is an animation of the GORDIAN KNOT here and also Nick Mee's animation in the sculpture section.)
© Mathematics and Knots/Edition Limitee 1996 - 2002
This material may be used freely for educational, artistic and
scientific purposes, but may not be used for commercial purposes,
for profit or in texts without the permission of the publishers.