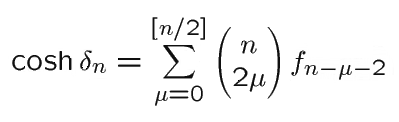
It is known [H.S.M. Coxeter, 'Loxodromic Sequences of Tangent Spheres', Æquationes Mathematicæ, 1 (1968), pp. 112-117] that, for a sequence of circles s_n such that every 4 consecutive members are mutually tangent, the inversive distance d _n between s₀ and s_n (or between s _m and s _m+n for any m ) is given in terms of the Fibonacci numbers f_n : 1, 1, 2, 3, 5, ..., by the formula

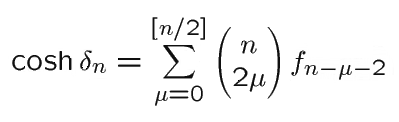
For the analogous sequence of spheres, such that every 5 consecutive members are mutually tangent, a prize is offered to the first person who provides the analogous formula for the inversive distances between pairs of the spheres. Meanwhile, by taking one pair of adjacent 'spheres' to be a pair of parallel planes, one easily finds that the values of cosh d_n are

John Robinson's sculpture FIRMAMENT is based on seven such spheres whose radii are in geometric progression; that is, the seven radii are proportional to

where x is the root, between 1 and 2, of the quintic equation x⁵ - x⁴ - x³ - x² - x + 1 = 0. This equation has a root -1 and the remaining quartic is easily solvable as a quadratic in x + 1/x to give x as

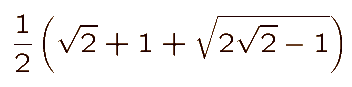
or approximately 1.8832. This gives the radii previously described.

Donald Coxeter, January 1997