Knots

For mathematicians, the first study is the form of a knot, since other properties of interest to a practical knot tyer, as in the Ashley Book of Knots, are difficult to deal with mathematically, and in any case require first an understanding of form.

The knot cannot be untied without cutting the string, or letting go of one end. Since one gets tired of holding both ends, one ties them together to form a loop, so obtaining thetrefoil knot, or its mirror image.

We have developed an Exhibition which shows how Mathematics gets into Knots, and which is also on this site. Our pages on Torus Knots show some of the mathematics which John intuited in making his sculptures. In the following pictures, we see the sculpture CONSCIENCE contains the form of a trefoil knot.

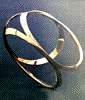
These pictures show that the sculpture CONSCIENCE can be transformed into a Trefoil knot.

Another trefoil knot used by John is in IMMORTALITY. This is more than a trefoil knot, it is actually a Möbius Band knotted into a trefoil. So it combines two mathematical themes discussed in these pages, knots and fibre bundles. Read again John's description of how he made IMMORTALITY to see this combination. Nick Mee of Virtual Image (outside link) has made a beautiful moving image (220KB). Here it is:

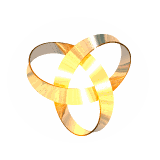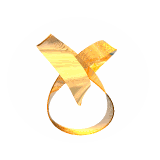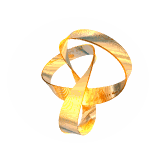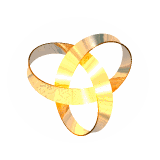
You will find other fascinating examples of Möbius Bands and twisted structures in Tom Longtin's pages (outside link). You will also find lots about knots in Knot Plot Site (outside link).