Flying around a Knot

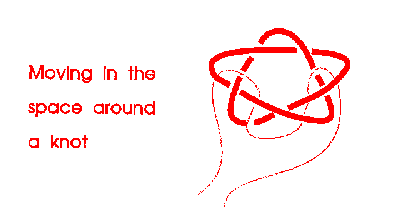
Here we investigate the space around a knot.

Mathematical notions of space are of use for representing motion, and change.

To investigate a space, you move around it.

As you do so, you carry some string to show where you have been.

Now we introduce some algebra: a product or composition of loops.

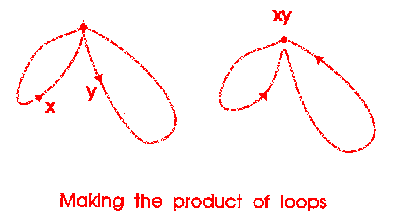
Now we relate this to the structure of the knot.

Here is how the product works - do one loop, and then another:

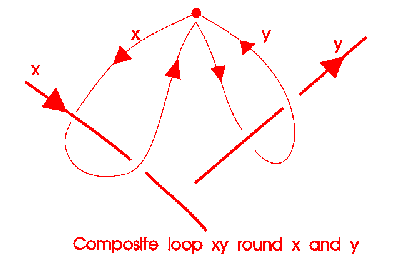
This product is associative.

Also we have inverses.

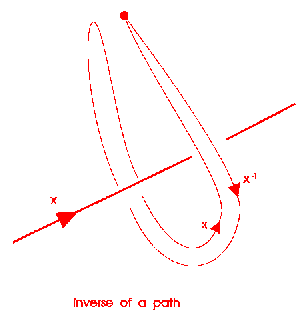
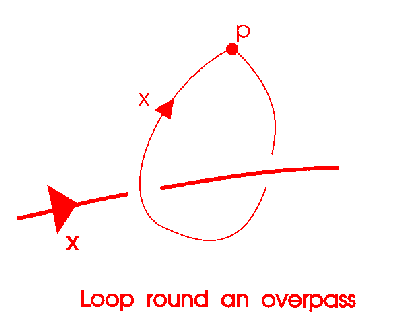
Now we explain how the crossings fit in.

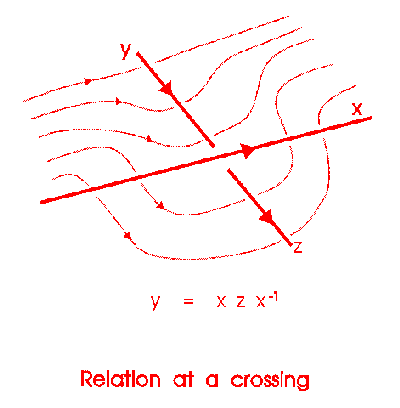
Using these relations at each crossing for a cinquefoil

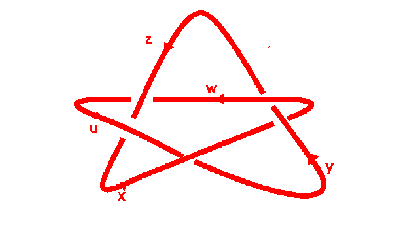
we end up with:

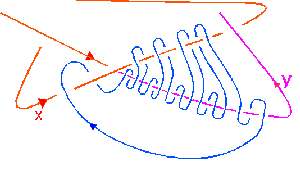
If you wrap a loop of string around the pentoil according to the above rule as shown, then it may be taken off without cutting, by pulling the loop over the other crossings.  The form of the above rule is a kind of invariant of the knot. For the trefoil knot, one obtains the rule

This distinguishes the pentoil from the trefoil. Other knots need more letters and more rules.

How are these formulae obtained? We give an explanation of where they come from.