The MÖBIUS BAND
and
The Projective Plane
(Page 2 of 2)
 |
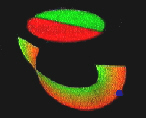 |
We
gradually deform the remainder so that it becomes more like a strip.
Now we can glue together those parts of this strip which should have
have been glued as part of the hemisphere.
|
So
there has to be a twist as we glue, and we get the famous Möbius
Band. We have replaced our original picture of a moving pivoted rod in
3-dimensional space by a point (or disc) moving on a space which
consists of a Möbius Band and a disc.
|
|
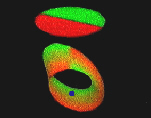 |
The edges of the disc
and the Möbius Band are circles, and these circular edges are to
be thought of as glued together. Again, we cannot do this gluing or
sewing in our real three dimensional space, but we illustrate it by
showing our moving disc hopping instantaneously from the edge of the
Möbius Band to the disc, and back again.
 |
|
This
picture of our mathematical space is convenient for representing types
of motion of our pivoted rod. The moving disc now leaves a trail, which
joins up to form what we call a loop. This loop represents a regular
and repetitive motion of the original rod.
|
 |
|

|
|
 |
| The
loop expands off the Möbius Band, |
|
onto the
disc,and finally down to a point.
|
|
This
point corresponds to a stationary rod. |
Now we can deform the
loop to show different motions. The movement of this loop shows how our
two parts of the space are joined. It also shows us the advantages of
the new picture: the changes of types of motion are more easily
represented in our new model than in our original picture. Our new
model allows for a global picture of particular motions of the rod in
3-dimensional space.
Another important
aspect is that the movements of this loop not only describe different
motions, but also give us information on the mathematical space which
represents the positions of the rod. We are interested not only in
movements, but in movements of movements, and so on, and this is an
intimation of a higher dimensional theory, of which there is much still
to be understood.
As part of our sequence
of pictures, we have a loop which goes twice round the Möbius
Band, and then this loop is deformed off the band and over to the disc,
and then to a small loop, and finally to a point, which represents a
stationary rod. This is related to the famous Dirac String Trick.
Mathematicians need to
progress to the representation of more complicated situations, which
arise in applications. The approach through studying `phase space',
that is the space representing all possible positions, has proved very
useful. Good visualisation of the simple examples is important for
using analogy to study the wider examples. We also need some general
methods. The notion of fibre
bundle has proved a convenient tool for representing many
complicated spaces.
Video
These pictures were
taken from a 4 min silent video, Pivoted lines and the Möbius
Band, produced in 1992 with a story line by Ronald Brown and
programmed at IBMUK Research by Ramen Sen. This video was a part of
Ronald Brown's Royal Institution Friday Evening Discourse, 'Out of
Line', May, 1992. The video was copyright IBM/Mathematics and Knots.
Copies of the video are no longer available, but there is now a cheaper
and better way of viewing it. A QT movie made from the video can be
found on the CDRom Raising
Public Awareness of Mathematics.
Projective Plane 1 | Dirac String Trick | The Brehm Model

© Mathematics
and Knots/Edition Limitee 1996 - 2002
This
material may be used freely for educational, artistic and scientific
purposes, with acknowledgement, but may not be used for commercial
purposes, for profit or in texts without the permission of the
publishers.








