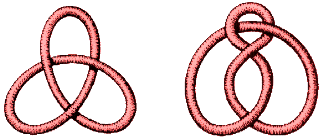Crossovers
In drawing pictures of knots, we represent lace and interlace by crossings. The more crossings there are the more complicated is the picture.
Here is a picture of a trefoil with nine crossings. By twisting
and crumpling, you can make a picture of a knot with as many crossings
as you can draw! So to find out about any knot, it is natural
to look for a picture of it with the smallest number of crossings.
The number of crossings in that picture is called the crossing number of the knot.



The unknot has crossing number 0. Any picture with only 1 or 2 crossings must be the unknot. Can you see why? We have not drawn all the knot pictures with 2 crossings, and
leave you to draw all those with 2 or with 3 crossings.

The trefoil has crossing number 3. On another page, we give a
diagram of a trefoil with 4 crossings. The figure eight has crossing number 4. Classifying knots according
to crossing numbers is one method of trying to understand the
infinite complications of knots and tangles.