Just how knotted is a knot? One measure of knottedness is the unknotting number of a knot. It is the smallest number of crossing changes needed to obtain the unknot from some diagram of the knot. The unknotting number is hard to calculate and remains unknown for many knots.
A crossing change looks like this:
The trefoil has crossing number 3 but can be unknotted by one change, so it has unknotting number 1
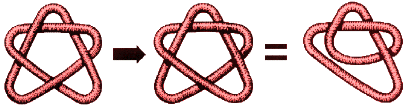
For the cinquefoil we need two changes. Here is a first. Either crossing can then
be changed for the second.. So it has unknotting number 2, though crossing number 5.
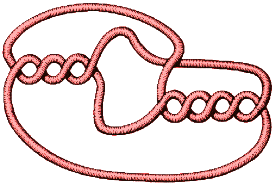
It was shown as recently as 1983 that the simplest diagram of
a knot is not necessarily the easiest to unknot! This knot has
10 crossings. It cannot be drawn with fewer, so it has crossing number 10. However to unknot this diagram we have to change 3 crossings.
Even so it does not have unknotting number 3 because ...
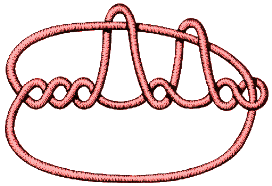
here is a different picture of the same knot with 14 crossings. We can change 2 crossings here to obtain the unknot. Our knot therefore has unknotting number 2. So the degree of unknottedness does not always arise in the simplest
picture of a knot. Question: which 2 crossings?! Those who have difficulty with this should stare at the complicated
example of the unknot on the page When are two knots the same?
Invariants
© Mathematics and Knots, U.C.N.W.,Bangor, 1996 - 2002
This material may be used freely for educational, artistic and
scientific purposes, but may not be used for commercial purposes,
for profit or in texts without the permission of the publishers.